Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems.[1] The Hubbard model, named after John Hubbard, is the simplest model of interacting particles in a lattice, with only two terms in the Hamiltonian (see example below): a kinetic term allowing for tunneling ('hopping') of particles between sites of the lattice and a potential term consisting of an on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, when the model is referred to as either the 'Bose–Hubbard model' or the 'boson Hubbard model'.
The Hubbard model is a good approximation for particles in a periodic potential at sufficiently low temperatures that all the particles are in the lowest Bloch band, as long as any long-range interactions between the particles can be ignored. If interactions between particles on different sites of the lattice are included, the model is often referred to as the 'extended Hubbard model'.
The model was originally proposed (in 1963) to describe electrons in solids and has since been the focus of particular interest as a model for high-temperature superconductivity. More recently, the Bose-Hubbard model has been used to describe the behavior of ultracold atoms trapped in optical lattices. Recent ultracold atom experiments have also realised the original, fermionic Hubbard model in the hope that such experiments could yield its phase diagram.[2]
For electrons in a solid, the Hubbard model can be considered as an improvement on the tight-binding model, which includes only the hopping term. For strong interactions, it can give qualitatively different behavior from the tight-binding model, and correctly predicts the existence of so-called Mott insulators, which are prevented from becoming conducting by the strong repulsion between the particles.
Contents |
Theory (Narrow energy band theory)
The Hubbard model is based on the tight-binding approximation from solid state physics. In the tight-binding approximation, electrons are viewed as occupying the standard orbitals of their constituent atoms, and then 'hopping' between atoms during conduction. Mathematically, this is represented as a 'hopping integral' or 'transfer integral' between neighboring atoms, which can be viewed as the physical principle that creates electron bands in crystalline materials, due to overlapping between atomic orbitals. Width of the band depends upon the overlapping amplitude. However, the more general band theories do not consider interactions between electrons explicitly. They consider interaction of a single electron with potential of nuclei and other electrons in the average way only. By formulating conduction in terms of the hopping integral, however, the Hubbard model is able to include the so-called 'onsite repulsion', which stems from the Coulomb repulsion between electrons at the same atomic orbitals. This sets up a competition between the hopping integral, which is a function of the distance and angles between neighboring atoms, and the on-site Coulomb repulsion, which is not considered in the usual band theories. The Hubbard model can therefore explain the transition from metal to insulator in certain transition metal oxides as they are heated by the increase in nearest neighbor spacing, which reduces the 'hopping integral' to the point where the onsite potential is dominant. Similarly, this can explain the transition from conductor to insulator in systems such as rare-earth pyrochlores as the atomic number of the rare-earth metal increases, because the lattice parameter increases (or the angle between atoms can also change — see Crystal structure) as the rare-earth element atomic number increases, thus changing the relative importance of the hopping integral compared to the onsite repulsion.
Example: 1D chain of hydrogen atoms
The hydrogen atom has only one electron, in the so-called s orbital, which can either be spin up ( ) or spin down (
) or spin down ( ). This orbital can be occupied by at most two electrons, one with spin up and one down (see Pauli exclusion principle).
). This orbital can be occupied by at most two electrons, one with spin up and one down (see Pauli exclusion principle).
Now, consider a 1D chain of hydrogen atoms. Under band theory, we would expect the 1s orbital to form a continuous band, which would be exactly half-full. The 1-D chain of hydrogen atoms is thus predicted to be a conductor under conventional band theory.
But now consider the case where the spacing between the hydrogen atoms is gradually increased. At some point we expect that the chain must become an insulator.
Expressed in terms of the Hubbard model, on the other hand, the Hamiltonian is now made up of two components. The first component is the hopping integral. The hopping integral is typically represented by the letter t because it represents the kinetic energy of electrons hopping between atoms. The second term in the Hubbard model is then the on-site repulsion, typically represented by the letter U because it represents the potential energy arising from the charges on the electrons. Written out in second quantization notation, the Hubbard Hamiltonian then takes the form:
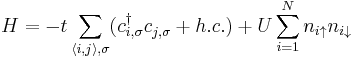 , where
, where 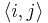 represents nearest-neighbor interaction on the lattice.
represents nearest-neighbor interaction on the lattice.
If we consider the Hamiltonian without the contribution of the second term, we are simply left with the tight binding formula from regular band theory.
When the second term is included, however, we end up with a more realistic model that also predicts a transition from conductor to insulator as the inter-atomic spacing is increased. In the limit where the spacing is infinite (or if we ignore the first term), the chain simply resolves into a set of isolated magnetic moments. Additionally, when there are some contributions from the first term, but the material remains an insulator, the overlap integral provides for exchange interactions between neighboring magnetic moments which may lead to a variety of interesting magnetic correlations, such as ferromagnetic, antiferromagnetic, etc. depending on the exact solutions of the model. One dimensional Hubbard model was solved by Lieb and Wu by means of Bethe ansatz. During 1990-2000 essential progress has been achieved: a hidden symmetry was discovered, the scattering matrix, correlation functions, thermodynamic and quantum entanglement were evaluated, see.[3]
More Complex Systems
Although the Hubbard model is useful in describing systems such as a 1-D chain of hydrogen atoms, it is important to note that in more complex systems there may be other effects that the Hubbard model does not consider. In general, insulators can be divided into Mott-Hubbard type insulators and charge transfer insulators.
Consider the following description of a Mott-Hubbard insulator:
- (Ni2+O2-)2 --> Ni3+O2- + Ni1+O2-
This can be seen as analogous to the Hubbard model for hydrogen chains, where conduction between unit cells can be described by a transfer integral.
However, it is possible for the electrons to exhibit another kind of behavior:
- Ni2+O2- --> Ni1+O1-
This is known as charge transfer, and results in charge transfer insulators. Note that this is quite different from the Mott-Hubbard insulator model because there is no electron transfer between unit cells, only within a unit cell.
Both of these effects may be present and competing in complex ionic systems.
Numerical treatment
The fact that the Hubbard model cannot be solved analytically in arbitrary dimensions has led to intense research into numerical methods for these strongly correlated electron systems.[4]
Exact treatment of the Hubbard model at absolute zero is possible using the Lanczos algorithm, which produces static as well dynamic properties of the system. This method requires the storing of three vectors of the size of the number of states, which limits the number of sites in the lattice to about 20 on currently available hardware. With projector and finite-temperature auxiliary field Monte Carlo two statistical methods exist that also can provide an exact solution. For low temperatures and large lattice sizes convergence problems appear that lead to an exponential growth of computational effort due to the so-called sign problem. The Hubbard model can also be studied within dynamical mean field theory (DMFT). This scheme maps the Hubbard Hamiltonian onto a single site impurity model, which allows one to compute the local Green's function of the Hubbard model for a given  and a given temperature. Within DMFT, one can compute the evolution of the spectral function and observe the appearance of the upper and lower Hubbard bands as correlations increase.
and a given temperature. Within DMFT, one can compute the evolution of the spectral function and observe the appearance of the upper and lower Hubbard bands as correlations increase.
See also
- Bloch wave
- Electronic band structure
- Solid state physics
- Bose–Hubbard model
- t-J model
- Dynamical Mean Field Theory
References
- ^ Alexander Altland and Ben Simons (2006). "Interaction effects in the tight-binding system". Condensed Matter Field Theory. Cambridge University Press. pp. 58 ff. ISBN 9780521845083. http://books.google.com/books?id=0KMkfAMe3JkC&pg=RA4-PA58.
- ^ Jorge Quintanilla and Chris Hooley (2009). "The strong-correlations puzzle". Physics World 22: 32–37. http://physicsworldarchive.iop.org/index.cfm?action=summary&doc=22%2F06%2Fphwv22i06a38%40pwa-xml&qt=%28quintanilla%20%3Cin%3E%20%28name%29%29.
- ^ The One-Dimensional Hubbard Model by Fabian H. L. Essler , Holger Frahm, Frank Göhmann, Andreas Klümper and Vladimir Korepin
- ^ Scalapino, Douglas J. (2006). "Numerical Studies of the 2D Hubbard Model". arXiv:cond-mat/0610710 [cond-mat].
External links
- Electron Correlations in Narrow Energy Bands, J. Hubbard, Proc. Roy. Soc. A 276 238 (1963)
- The one-dimensional Hubbard model - A reminiscence by E.H. Lieb and F.Y. Wu
- Generalized Hartree-Fock Theory and the Hubbard Model by V. Bach, E. H. Lieb, and J. Solovej
- The Hubbard Model: Some Rigorous Results and Open Problems by E.H. Lieb
- The One-Dimensional Hubbard Model by Fabian H. L. Essler , Holger Frahm, Frank Göhmann, Andreas Klümper and Vladimir Korepin
- Some Results and Publication of Vladimir Korepin
- The strong-correlations puzzle by J. Quintanilla and C. Hooley
- The Mott metal insulator transitions by Florian Gebhard
|
||||||||